-
-
Wie kann man sich den vierdimensionalen Raum vorstellen? Das können wir nicht - nicht im üblichen Sinn. Geometer, Mathematiker und Physiker können durch Analogieschlüsse Eigenschaften von vier- und höherdimensionalen Objekten erarbeiten.
Vierdimensional - was bedeutet das?
Zweidimensional
Die Lage eines Punktes P in der Ebene ist durch seine zwei Koordinaten x und y festgelegt. P(2/5) bedeutet, dass man zu P vom Ursprung aus gelangt, indem an zuerst entlang der x-Achse 2 Einheiten geht und dann parallel zur y-Achse 5 Einheiten. Da man zwei Koordinaten benötigt, nennt man die Ebene auch "zweidimensional", auch kurz R2. Die Abkürzung "R" kommt daher, da die Koordinaten reelle Zahlen sein können.
Dreidimensional
Ein Punkt P im Raum (R3) ist durch drei Koordinaten festgelegt, z.B. P(2/5/6,3).
Vierdimensional
Rein mathematisch und formal lässt durch Angabe von vier Zahlen ein Punkt im R4 beschreiben, z.B. P(2/5/6,3/9) - und natürlich können die Mathematiker in diesem R4 auch rechnen, z.B. Abstände zwischen zwei Punkten bestimmen.
Doch wie kann man sich so einen Punkt vorstellen? Gleich vorweg: Das können wir Menschen nicht. Wir können uns nur durch Analogieschlüsse Eigenschaften von vier- und höherdimensionalen Objekten erarbeiten.
Beispielhaft sollen Eigenschaften und sogar das Bild eines vierdimensionalen Würfels erarbeitet werden.
Wie zeichnen wir einen Würfel im R4?
Um zu verstehen, wie das Bild eines Würfels im R4 aussehen kann, beginnen wir mit dem Bild eines zweidimensionalen "Würfels" - mit dem Bild eines Quadrats also. Die Mathematiker nennen einen Würfel im R4 übrigens auch "Überwürfel" oder "Hyperwürfel" (engl. auch "Tesseract")
Lade dazu das Arbeitsblatt "Quadrat - Würfel - Überwürfel" herunter und drucke es aus!
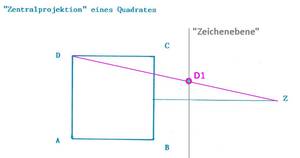
Aufgabe 1: Das Quadrat soll aus dem Punkt Z aus betrachtet werden oder anders gesprochen: Projiziere das Quadrat aus dem Punkt Z auf eine Gerade, die hier "Zeichenebene" genannt worden ist, obwohl es ja nur eine Gerade ist.
Eine Lösungsanregung findest du im kleinen Bild (hier herunterladbar).
Zur Kontrolle die Lösung: Die Lösung kann man hier einsehen.
Analyse der Lösung: Das Quadratbild wird durch die Bilder der vier Eckpunkte festgelegt A1, B1, C1, D1. Die vier Quadratseiten scheinen im Bild wieder auf, sind aber unterschiedlich lang: A1,B1 | A1,D1 | C1,D1 Wo ist die vierte Seite? (Das ist natürlich die Verbindung B1,C1.)
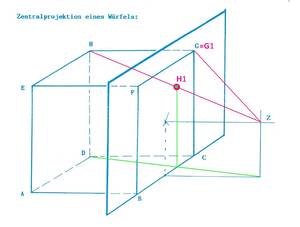
Noch eine Vorübung: Zentralprojektion eines Würfels im R3
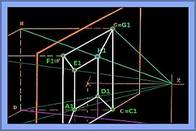
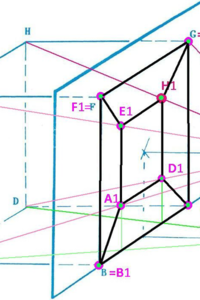
Aufgabe 2: Konstruiere nun die Zentralprojektion des Würfels ABCD EFGH aus dem Punkt Z auf die eingetragene Ebene. Ein Lösungsanregung findest du im Bild rechts.
Die Lösung kannst du hier herunterladen.
Analyse des Bildes: Das Würfelbild besteht also aus 8 Eckpunkten A1,B1,C1, ... Die Zentralprojektion erscheint etwas verzerrt. Aber ich denke, du erkennst, dass das Zentralbild des R3-Würfels aus zwei ineinander verschachtelten Quadraten besteht: Wenn man genau hinsieht, dann erkennt man die Bilder aller 6 Seitenflächenquadrate: Das Quadrat ADHE wird auf das kleine Quadrat A1,D1,H1,E1 abgebildet. Das Quadrat BCGF bleibt unverändert, da es in der Bildebene liegt. Die vier anderen Quadrate werden durch die Zentralprojektion verzerrt und sind im Bild Trapeze.
Wir fassen zusammen: Alle 8 Eckpunkte, alle 6 Seitenflächen (und natürlich auch alle 12 Kanten) des Würfels sind im Bild eindeutig erkennbar.
Nun sind wir bereit für das Herunterladen einer Zentralprojektion eines Überwürfels ...
Wieviel Eckpunkte kannst du erkennen? Wieviele Seitenkanten? Wieviele Seitenwürfel?
Ja, die Oberfläche eines Hyperwürfels besteht tatsächlich aus R3-Würfeln, nur der innere und äußere Würfel erscheinen (wie im Beispiel oben) wieder in der Form eines Würfels.
Überwürfel in Kunst und Architektur
... auch das gibt es
Salvator DALI malte sein berühmtes surrealistisches Bild im Jahre 1954:
Suche im Internet nach den Schlagwörten salvator dali hypercubus
Wie hängt dieses Bild mit dem R4 zusammen?
In welchem Museum findet man das Original?
In Paris findet sich der Grande Arche (in La Defense), ein zu einem architektonischen Meilenstein in Paris gewordener Überwürfel.
Suche im Internet nach La Grande Arche und du wirst viele Bilder davon finden.
Wie heißen die Architekten dieses mehr als 100 Meter hohen Bauwerks in Paris?
Punkte im R4 zeichnen?
Ja, auch das kann man - und zwar mit einer lange bewährten Methode der Darstellenden Geometrie.
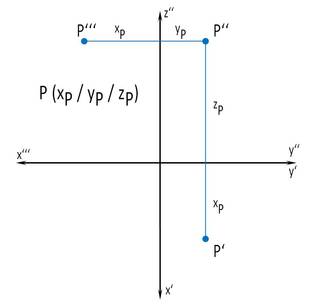
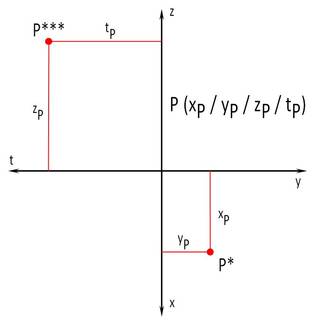
Links unten sieht man die Darstellung eines Punktes P im dreidimensionalen Raum im Grund-Auf- und Kreuzriss (Näheres dazu findest du im Lernpaket "Hauptrisse erzeugen"). Rechts daneben wird gezeigt, wie man einen Punkt im R4 - festgelegt durch vier Koordinaten - in zwei unabhängigen Koordinatenfeldern (x,y) und (z,t) darstellen kann. Natürlich kann man sich dann auch Konstruktionen, wie die Konstruktion des Abstandes zwischen zwei R4-Punkten, überlegen.
Bemerkung: Die vierte Dimension wird auch mit "t" bezeichnet - abgeleitet aus der Abkürzung für die Zeit, wie sie in der Physik verwendet wird.
Ein High-School-Student erklärt den R4 (engl.)
Flächenland
Einen reizvollen Zugang zum Verständnis des R4 bietet das Buch "Flächenland" von Edwin A. Abbott - schon im Jahre 1884 als gesellschaftskritischer Roman in England erschienen. Der englische Originaltext ist zum Beispiel hier im Netz anzusehen:
Im Buch erzählt ein Bewohner von Flächenland (R2) von einem Besucher aus dem Raum (R3). Die wichtigsten Passagen des ersten Zusammentreffens der Beiden sind im "Knaurs Buch der moderenen Mathematik" von Walter R.Fuchs (1966) trefflich ausgewählt und können hier eingesehen werden.
Ein 5-Minuten Trickfilm über Flächenland kann hier eingesehen werden:
Flächenland von Abbott wurde auch verfilmt. Den Film (1:39) kann man sich auf Youtube ansehen.
Filmserie über die Dimensionen