-
-
Das kannst du hier lernen:
- Was ist "Axonometrie"?
- Warum gibt es genormte Abbildungen?
- Welche solcher Abbildungen sieht die ÖNORM vor?
- Wann setze ich welche Abbildungen ein?
Was ist "Axonometrie"?
Axonometrie ist eine Methode, um räumliche Objekte durch eine Parallelprojektion anschaulich darzustellen. Der besondere "Trick" dabei ist, dass man den Umweg über ein räumliches Koordinatensystem wählt.
Praktisch bedeutet dies, dass man im
Schritt 1: zuerst "Hauptrichtungen" (möglichst jeweils normal zueinander) am Objekt sucht, dann ein Raumkoordinatensystem in diese Hauptrichtungen legt. Vergleiche dazu die beiden Bildleisten unterhalb!
Danach zeichnet man im
Schritt 2: die Bilder der drei Koordinatenachsen auf das Zeichenblatt und ergänzt danach die Bilder der Kanten des Objektes.
Da eine Parallelprojektion vorliegt, beachtet man beim Zeichnen des Bildes die Gesetze dieser Abbildung, im wesentlichen also die "Parallelentreue" (Parallele Kanten am Raumobjekt sind im Bild wieder parallel.) und die "Teilverhältnistreue" (Bilder der Teilungspunkte von Raumstrecken teilen die Bildstrecken im gleichen Verhältnis wie im Raum.)

- Hauptrichtungen an realen Objekten

- Hauptrichtungen an Würfelobjekten
Was sind "Spezialfälle" der Axonometrie?
Spezielle Axonometrien entstehen nun durch die Wahl besonderer Winkel zwischen den Bildern der Koordinatenachsen x, y und z.
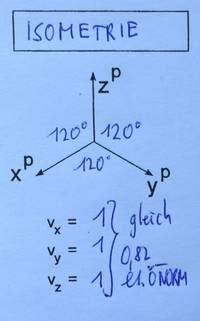
Sind etwa alle drei Winkel gleich (120°), so spricht man von einer isometrischen Darstellung oder kurz "Isometrie" (iso... gleich).
In der Praxis der technischen Zeichner wurden einige besondere Ansichten mit eigenen Namen versehen und die zu wählenden Winkel und Verzerrungen der Achsenlängen durch die ÖNORM (Nr. 6061) und deren Nachfolgernormen festgelegt.
Aufgabe: Damit du eine gute Übersicht erhalten kannst, lade dir das Arbeitsblatt "Axonometrische Angaben: Spezialfälle" herunter, drucke es aus und ergänze es nach den hier vorliegenden Informationen.
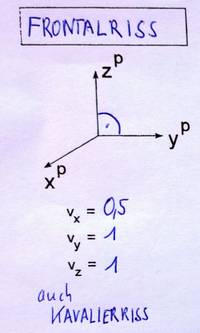
Frontalriss
-
-
Kennzeichen:
- Winkel zwischen yP und zP ist 90°
- Alle Figuren in der yz-Ebene und parallel dazu erscheinen unverzerrt.
Laut ÖNORM sollte der Winkel zwischen xP und yP 45° und die Verzerrung der x-Achse 0,5 betragen. Da Normen keine verbindlichen Gesetz darstellen, können diese Werte beim praktischen Zeichnen auch verändert sein.
Veralteter Name: Kavalierriss ("Kavaliere" hießen die großen Festungstürme hinter einer Stadtmauer. Diese sind bei dieser Darstellungsart besonder gut zu sehen.)
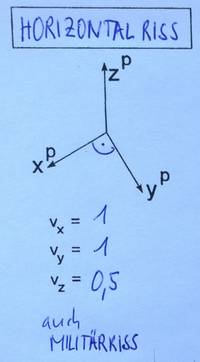
Horizontalriss
-
-
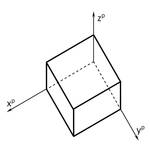
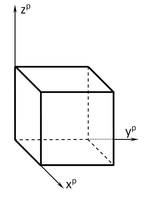
- Würfel im Horizontalriss
Kennzeichen:
- Winkel zwischen xP und yP ist 90°
- Alle Figuren in der xy-Ebene und parallel dazu erscheinen unverzerrt.
Laut ÖNORM sollte der Winkel zwischen xP und zP 120° und die Verzerrung der z-Achse 0,5 betragen. Da Normen keine verbindlichen Gesetz darstellen, können diese Werte beim praktischen Zeichnen auch verändert sein.
Veralteter Name: Militärriss (Der Name leitet sich aus der Darstellung von Festungsanlagen her.)
Isometrie
-
-
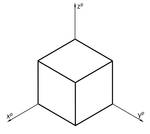
- Würfel in Isometrie
Kennzeichen:
- Winkel sind 120°
- Alle drei Koordinatenebene erscheinen (gleich) verzerrt.
Laut ÖNORM sollte die Verzerrung aller drei Achsen 0,82 betragen. Da Normen keine verbindlichen Gesetz darstellen, können diese Werte beim praktischen Zeichnen auch verändert sein. In der Praxis wählt man am besten die Verzerrung 1 (unverzerrt).
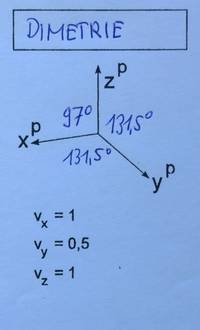
Dimetrie
-
-
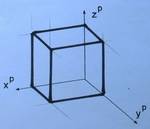
- Würfel in (vereinfachter) Dimetrie
Kennzeichen:
- Winkel zwischen yP und zP sowie zwischen yP und zP sind gleich (131,5°)
- Alle Figuren in den Koordinatenebene erscheinen verzerrt.
Laut ÖNORM soll die Verzerrung der y-Achse bei (vereinfachter) Dimetrie 0,5 sein, x- und z-Achse sind unverzerrt dargestellt.
Anderer Name: Kabinettprojektion
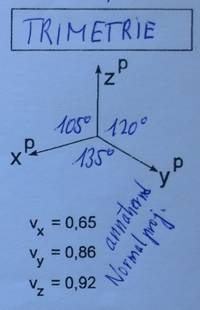
Trimetrie
-
-
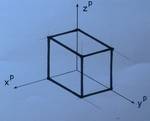
- Würfel in Trimetrie
Kennzeichen:
- Alle drei Winkel sind verschieden: 120° zwischen yP und zP, 105° zwischen xP und zP, 135° zwischen xP und yP
- Alle Figuren in den Koordinatenebene erscheinen verzerrt.
- Werden die laut ÖNORM vorgegebenen Verzerrungen (für x-Achse 0,65, für y-Achse 0,86 und für z-Achse 0,92) eingehalten, so ergibt sich annähernd eine Normalprojektion. (Dies hat große Vorteile bei Kreis-und Kugeldarstellungen)
Links zu Texten, Dokumenten und Videos