Bewegungen im Alltag

- Drehung

- Schiebung

- Drehung

- Drehung
Schon beim Öffnen einer Tür oder eines Backrohrs können Drehungen und Schiebungen in unserer Umwelt erkannt werden.
Übersicht über die Raumtransformationen
Schiebung, Spiegelung und Drehung werden zu den Raumtransformationen gezählt. Dabei sind natürlich nur Schiebungen und Drehungen echte Bewegungen im Raum. Eine Schraubung kann durch gleichzeitiges Ausführen von Drehung um eine Achse und Schiebung längs dieser entstehen.
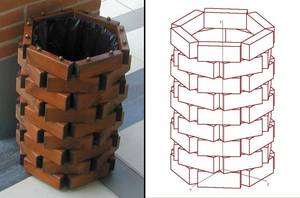
Anhand des dargestellen Objektes (Papierkorb), der aus lauter gleich großen Holzquadern (25 x 6 x 10 = l x b x h) aufgebaut ist, können alle diese Transformationen modellhaft veranschaulicht werden.
Schiebung (auch "Translation")
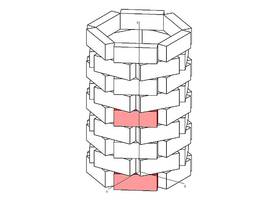
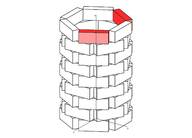
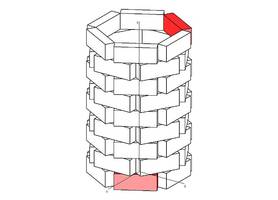
Wie kann beim rechts abgebildeten „Papierkorb“ der markierte Ausgangsbaustein unten in die obere (ebenfalls hervorgehobene) Lage gebracht werden?
Jeder einzelne Punkt des Quaders (z.B. der Mittelpunkt, jeder Eckpunkt) muss dazu in dieselbe Richtung um dieselbe Länge verschoben werden.
Die notwendige Transformation heißt Schiebung!
Alle Schiebungspfeile sind gleich lang, parallel und zeigen in dieselbe Richtung. Alle Schiebungspfeile bilden einen sogenannten Vektor.
Hinweis: Ein Vektor ist also eine unendliche Anzahl von Pfeilen! Im praktischen Sprachgebrauch sagt man allerdings oft nur zu einem einzigen dieser Pfeile schon „Vektor“.
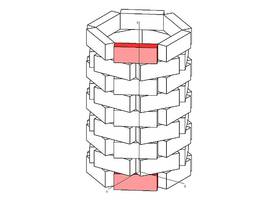
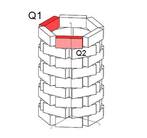
Eine weitere Schiebung
Wie lautet der Schiebungsvektor (Quaderhöhe = 10)?
(x / y / z ) = (0 / 0 / ...)
Drehung (auch "Rotation")
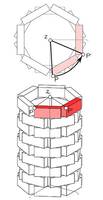
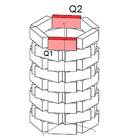
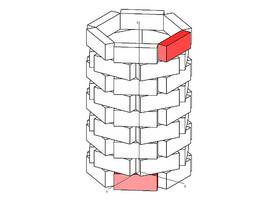
Blickt man von oben auf den Papierkorb („Grundriss“), dann erkennt man, dass jeder Punkt um den Mittelpunkt (= Grundriss der z-Achse) um 60° gedreht werden kann.
Eine Drehung liegt vor, wenn jeder Punkt um denselben Winkel um dieselbe Achse bewegt wird. Die Radien stehen jeweils normal zur Drehachse.
Eine Drehung ist durch die Achse, den Drehwinkel und den Drehsinn (im Uhrzeigersinn oder gegen den UZS) festgelegt.
Es ist mathematisch festgelegt ("definiert"), dass eine Drehung im Uhrzeigersinn mathematisch "negativ" (-) oder Rechtsdrehung genannt und gegen den Uhrzeigersinn mathematisch "positiv" (+) oder Linksdrehung genannt wird.
Weitere Drehungen
Drehachse = z-Achse. Gib jeweils Drehwinkel und Drehsinn an!
Spiegelungen
Bei Spiegelungen kann man im Raum zwischen Spiegelung an einer Ebene, an einer Geraden oder an einem Punkt unterscheiden. Je nachdem spricht man ein einer Ebenenspiegelung, einer Geradenspiegelung oder einer Punktspiegelung.
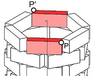
- Geradensp. (an z-Achse)
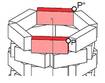
- Ebenensp.
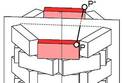
- Ebenensp. (Lösung)

- Ebenensp.
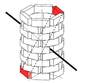
- Geradensp.
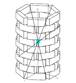
- Punktsp.
Schraubung
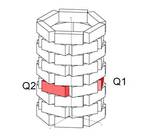
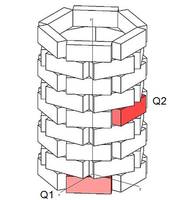
Der Quader Q2 geht hier aus dem Quader Q1 weder durch Schiebung noch durch Drehung hervor, sondern nur durch eine Kombination der beiden Transformationen. Zunächst denkt man sich eine Schiebung in z-Richtung um den Vektor (0/0/40), dann eine Drehung um den Winkel 60° um die z-Achse (+60° beim Blick gegen die z-Achse, -60° beim Blick in z-Richtung!)
Eine Schraubung ist zusammengesetzt aus einer Schiebung längs einer Geraden und gleichzeitiger Drehung um diese Achse. Deshalb benötigt man einen Schiebungsvektor und einen Drehwinkel samt Drehsinn (Rechtsdrehung bei Blick in Richtung des Schiebungsvektors fürht zu einer Rechtsschraubung, bei Linksdrehung handelt es sich um eine Linksschraubung.)
Weitere Schraubungen
Überlege jeweils Schiebungsvektor und Drehwinkel (bei Blick in Schiebrichtung)!
Übungsblatt zu den Raumtransformationen
Ein Übungsblatt zum praktischen Erkennen von Raumtransformationen kann man HIER herunterladen.