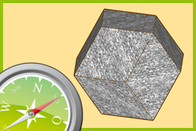
ePilot: Granatkapelle
Regelmäßige räumliche Strukturen spielen beispielsweise in der Mineralogie oder in der Chemie eine Rolle. Im Zillertal wurde früher das Mineralgestein Granat abgebaut. Ein Schweizer Architekt hat die besondere geometrische Form dieses Minerals für den Entwurf einer Kapelle verwendet.
Infos zum ePilot-Tipp
| Linktipp | Granatkapelle |
| Unterrichtsthema | Rhombendodekaeder als Beispiel für eine regelmäßige räumliche Struktur |
| Schulstufe | 7.-10. |
| Typ | Sachinformation, Unterrichtsidee, Veranschaulichung |
Das empfohlene Dokument enthält neben einigen Fotos und einer kompakten Information auch verschiedene Risse und Skizzen des Architekten. Damit können an diesem Bauprojekt die verschiedenen Planungsschritte und –stadien in altersadäquater Form nachvollzogen werden: Idee – skizzenhafte Entwürfe – exakte Pläne inklusive Lageplan – fertiges Bauwerk.
Idee zum Unterrichtseinsatz
Setzt man auf die sechs Flächen eines Würfels jeweils eine regelmäßige quadratische Pyramide, deren Höhe die halbe Kantenlänge des Würfels ist, so „verschmelzen“ benachbarte Pyramidenflächen zu Rhomben. Es entsteht ein Körper mit zwölf kongruenten Rhomben als Begrenzungsflächen, ein Rhombendodekaeder. Dieser Körper ist allerdings nicht ganz regelmäßig, weil die Winkel in den Ecken unterschiedlich sind. Deshalb zählt das Rhombendodekaeder nicht zu den fünf platonischen Körpern, die völlig regelmäßig sind.
Das Bauwerk könnte Anlass sein, die geometrischen Eigenschaften des Rhombendodekaeders genauer unter die Lupe zu nehmen. Ausgehend von Würfelbildern könnten durch „Aufsetzen“ der Pyramiden verschiedene Risse konstruiert werden. Mit geeigneter Software könnte das Objekt modelliert, in die der Kapelle entsprechende Lage gebracht und mit Sockel, Türe und eventuell Fenstern ausgestattet werden.
Anschließend könnten die in dem Dokument befindlichen Schnitte und Ansichten nachvollzogen werden. Die Anfertigung eines Modells (z. B. aus Zeichenkarton) könnte das kleine Projekt komplettieren.
Auch für Berechnungen eignet sich das Rhombendodekaeder. So kann leicht nachgerechnet werden, dass die sechs Pyramiden zusammen das gleiche Volumen wie der Ausgangswürfel haben. Mit Hilfe des Satzes von Pythagoras kann auch der Inhalt einer Pyramidenfläche und damit der ganzen Oberfläche berechnet werden
Fazit
Die Kinder gewinnen wesentlich motivierter und rascher Zugang zu geometrischen Sachverhalten, wenn diese an konkreten Objekten nachvollziehbar sind. Die vorliegende Kapelle stellt ein Bauwerk dar, dessen geometrische Form klar erkennbar und nicht zu komplex für eine kindgerechte Aufbereitung ist.
Die bevorstehende Ferienzeit bietet Gelegenheiten, Geometrisches in nah und fern zu entdecken und durch Fotos, Skizzen oder andere Medien für den Unterricht festzuhalten. Die methodische Aufbereitung kann dann später erfolgen, wenn es die Unterrichtsvorbereitung erfordert.
Viele geometrische Entdeckungen sowie natürlich einen erholsamen und an positiven Erlebnissen reichen Sommer wünscht Ihnen und Ihren Schülerinnen und Schülern
Ihr ePilot für Geometrisches Zeichnen
Manfred Blümel