Monge, Gaspard: Darstellende Geometrie
Sein klassisches Werk erschien 1798. Der Link führt zum Scan der deutschen Übersetzung von Robert Haussner, die 1900 in Leipzig (Verlag von Wilhelm Engelmann) herausgekommen ist.
Mehr zu Gaspard Monge (1746-1818), dem französischen Mathematiker, der als Vater/“Erfinder“ der klassischen darstellenden Geometrie gilt, finden Sie zB. unter http://en.wikipedia.org/wiki/Gaspard_monge
Der angegebene Link zu seinem Buch führt auf die Sammlung der University of Michigan. Dort wurde eine virtuelle Bibliothek klassischer historischer Mathematikbücher angelegt. (University of Michigan Historical Math Collection)
... und hier geht es zu einer französischen Fassung aus dem Jahre 1847
... und hier zu einer Ausgabe aus dem Jahre 1798 (in der Bibliothek der ETH Zürich)
Aus seinem Buch ...
Monge schreibt zu Beginn über die Aufgabe und Methode der darstellenden Geometrie: „Elementare Aufgaben. Aufgabe der darstellenden Geometrie. 1. Die Aufgabe der darstellenden Geometrie ist eine zweifache. Erstens soll sie die Methoden liefern, um auf einem Zeichenblatte, welches also nur zwei Dimensionen, Länge und Breite hat, alle Raumgebilde, welche deren drei, nämlich Länge, Breite und Höhe haben, abzubilden, vorausgesetzt, dass diese Gebilde streng definirt werden können.
Zweitens soll sie das Verfahren lehren, um aus einer genauen Zeichnung die Gestalt der Raumgebilde erkennen und alle Sätze, welche aus der Gestalt und der gegenseitigen Lage der Raumgebilde folgen, ableiten zu können.“
Ab Seite 172 sind Zusätze von Monge selbst und ab Seite 176 findet man Anmerkungen und historische Bemerkungen des Übersetzers.
Monge beendet sein Werk mit einem Satz über die Vorteile der neuen von ihm begründeten Wissenschaft, die „sowohl die Künste als die Industrie aus der Errichtung einer Schule für darstellende Geometrie in jedem Distrikte der Republik ziehen würden“.
Ein Beispiel...
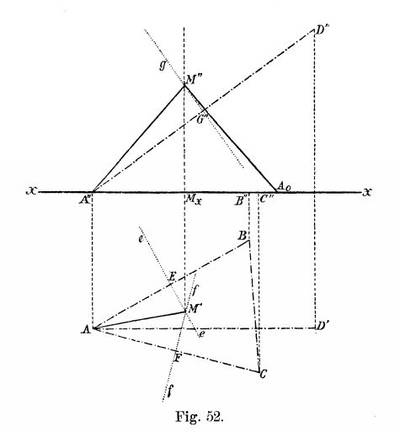
Etwa aus der Seite 123 (Fig 52, unten eingefügt): Konstruktion des Mittelpunktes einer Kugel, welche durch vier Punkt geht. Diese erfolgt durch Herstellen einer speziellen Ansicht der Lage der vier Punkte.
Lesen und sehen Sie selbst: Viele der Inhalte der klassischen DG-Ausbildung am Ende der 1900er Jahre scheinen bereits in diesem Werk von G. Monge auf.